( Number System )संख्याएँ क्या होती है ? एवं संख्याओं के सभी प्रकार

Number System में निम्न प्रकार की संख्याएँ होती है :-

 1.प्राकृतिक संख्याये 2.पूर्ण संख्याये 3.सम संख्याये 4 .विषम संख्याये 5.पूर्णांक संख्याये 6.परिमेय संख्याये 7.अपरिमेय संख्याये 8.रूढ़ या अभाज्य संख्याये 9.भाज्य संख्याये 10.सह-अभाज्य संख्याये

1. प्राकृतिक संख्या ( Natural Number ) :- 

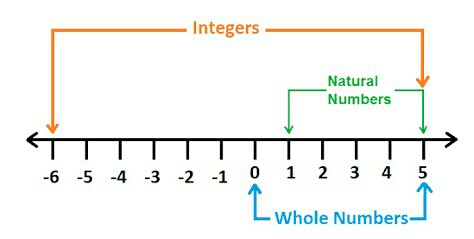
जो संख्या किसी वस्तु को गिनने के काम आती है वह प्राकृतिक संख्या है।

1,2,3,4,5,6…. ये सभी प्राकृतिक संख्या है।

1.2,1.5,-1,-2,0,1.11… ये सभी संख्या प्राकृतिक तौर पर गिनने के काम नहीं आती है, यानि की ये सभी प्राकृतिक संख्याएँ नहीं है |

Note :- 0 कोई प्राकृतिक संख्या नहीं है ।

2. पूर्ण संख्याएँ ( Whole Number ) :-

0 से अनन्त तक की सभी संख्याएँ पूर्ण संख्याएँ होती है ।

Ex :- 0,1,2,3,4,5,6,7.......

3. सम संख्या ( Even Number) :-

जो संख्या दो से भाग देने पर कट जाय वे सम संख्या कहलाती हैं।जैसे 2,4,6,8,10 ।

जिस संख्या के अन्त में 2,4,6,8,0 आयेगा वे सभी सम संख्या हैं।

4. विसम संख्या (Odd Number) :-

जो संख्या 2 से भाग देने पर न कटें जैसे 1,3,5,7,9 वे विषम संख्या हैं।

जिनके अन्त में 1,3,5,7,9 आयेगा वे विषम संख्या हैं।

Ex :- 11,13,15,17,19,21......

5. पूर्णांक संख्याएँ ( Integer Number ) :-

संख्या पद्धति में सभी पूर्ण संख्या  एवं ऋणात्मक संख्या साथ में मिलकर जो संगृह बनाते हैं वह संगृह पूर्णांक कहलाता है। 

जैसे:  -6, -9, -11, 10, 8, 7, 6, 0 आदि सभी पूर्णांक हैं।

6. परिमेय संख्याएँ ( Rational Number ) :-

ऐसी संख्या जो p/q के फॉर्म में हों,  या संख्या जिन्हें p/q

के रूप में व्यक्त किया जा सकता हो, जहाँ p तथा q पूर्णांक हों तथा q≠0 हो, परिमेय संख्यां कहलाती हैं।

Ex :- 1/2 , 4/7 , 3/-2 आदि परिमेय संख्या के उदाहरण है ।

7. अपरिमेय संख्या (irrational number) :-

अपरिमेय संख्या  वह वास्तविक संख्या है जो परिमेय नहीं है, अर्थात् जिसे भिन्न p /q के रूप में व्यक्त नहीं किया जा सकता है, जहां p और q पूर्णांक हैं, जिसमें q गैर-शून्य (अर्थात शून्य नहीं है )है और इसलिए परिमेय संख्या नहीं है।

➡हम ऐसा भी बोल सकते है कि अपरिमेय संख्या को एक सरल भिन्न के रूप में प्रदर्शित नहीं किया जा सकता

Ex :- π, e और √२ अपरिमेय संख्या है

8. Prime Number ( अभाज्य संख्या ) :-

अभाज्य संख्या वह संख्या होती है जो या तो खुद से या फिर 1 से Devide ( भाग ) हो ।

Ex  :-  2,3,5,7,11,13,17,19,23,29,31,........

Note :- 1 अभाज्य संख्या नहीं है क्योंकि यह सबसे                   गुना होती है 

➡ 1 से 100 के बीच अभाज्य संख्याएँ 

1 से 100   ➡ 25

1 से 25     ➡ 09

25 से 50   ➡ 06

50 से 100 ➡ 10

09 .Coprime Number ( सहअभाज्य संख्या ) :-

सहभाज्य संख्या ऐसी दो संख्याओं का समूह होता है जिनका HCF हमेशा 1 होना चाहिए ।

➡ HCF हमेशा 1 होना चाहिए ( 1 के अलावा दोनों में कुछ भी कॉमन नहीं होना चाहिए )

Ex:- ( 4,5) सहभाज्य संख्या है

10. Composit Number ( भाज्य संख्याएँ ) :-

जो अभाज्य संख्या नहीं है वह सभी भाज्य संख्या है

Ex:-  4,6,8,9,10,12,14...........

Note  :- 1 भाज्य संख्या नहीं है

11. Triangular Number ( त्रिकोणीय संख्याएँ ) :-

ऐसी संख्याएँ जो त्रिकोण बनाती है त्रिकोणीय संख्याएँ कहलाती है ।

इस फॉर्मूले से त्रिकोणीय संख्याओं को हम निकाल सकते है ।

➡ n वी त्रिकोणीय संख्या = n(n+1)/2

Ex :- 15 वी त्रिकोणीय संख्या = 15(15+1)/2

                                         = 120

इसे सिंपल आप इस तरह से याद रख सकते है की n प्राकृत संख्याओं का योग भी यही होता है ।

➡ n प्राकृत संख्याओं का योग = n(n+1)/2

दोस्तों इसी तरह के Blog के लिए आप FaduStudy Blog को फॉलो कर सकते है जिससे आने वाले सभी Blogs का अपडेट आपको मिलता रहेगा ।

इस तरह के वीडियोस देखने के लिए आप हमारे FaduStudy यूट्यूब चैनल को भी सब्सक्राइब कर सकते है